Cuadrados Mágicos y Recursión

En las matemáticas hay muchos problemas que son básicamente recreativos. Uno de ellos es el de los cuadrados mágicos, en donde se trata de colocar números en una matriz de celdas de n x n, de forma tal que la suma de los números por columnas, filas y diagonales principales sea la misma, la constante mágica. Usualmente los números empleados para rellenar las casillas son consecutivos, de 1 a n², siendo n el número de columnas y filas del cuadrado mágico.

Estos cuadrados se conocen ya en la antigua China, desde el III milenio A.C. Hay también referencias a los mismos en las culturas india, egipcia, árabe y griega. Y aunque muchas veces se han asociado con cuestiones astrológicas o de índole mágico, la realidad es que es una simple recreación matemática que es interesante por sí misma.

El artista renacentista Alberto Durero, en su obra Melancolía I, incluye un cuadrado mágico de orden 4 (4x4 celdas), en donde la constante mágica es 34. La figura 1 tiene los valores de dicho cuadrado.

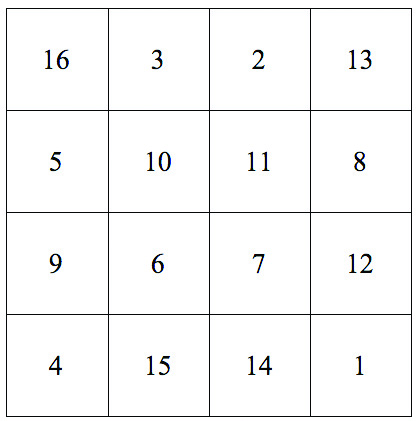
Figura 1. El cuadrado mágico de Durero.

Existen una serie de procedimientos para crear cuadrados mágicos de orden par o impar. Un ejercicio interesante es escribir un programa que siga estos procedimientos para generar cualquier cuadrado mágico. No obstante esto, la pregunta que surge es si se puede generar un cuadrado mágico a prueba y error, sin necesidad de conocer algoritmo alguno. La respuesta es: sí, y para ello lo mejor que podemos hacer es usar un lenguaje de programación al que se le den los datos correspondientes y el programa resuelva automáticamente lo que buscamos. Este tipo de lenguajes declarativos forman un paradigma diferente al de los lenguajes imperativos y Prolog es uno de los mejores ejemplos del mismo.

Prolog nació en los años 70 del siglo pasado, en la Universidad de Aix-Marseille I (Francia), ideado por dos estudiantes, Alain Colmerauer y Philippe Roussel. La primera versión del lenguaje se escribió en Algol 60 y era interpretado. Más tarde (1983), llegaría David H.D. Warren, quien habría desarrollado un compilador que traducía Prolog en una serie de instrucciones de una máquina virtual, la cual se denominó a la postre la Máquina Abstracta de Warren (también conocida como WAM - Warren Abstract Machine).

Los programas en Prolog se componen de cláusulas de Horn que constituyen reglas del tipo “modus ponendo ponens”, es decir, “si es verdad el antecedente, entonces es verdad el consecuente”. Básicamente Prolog usa hechos y reglas. Los hechos son verdades que son ciertas en el entorno de un programa y las reglas definen verdades cuando se cumplen una serie de hechos. Prolog se basa así, en inferencias lógicas. A manera de ejemplo, si me presentan a alguien que se llama Jorge Flores y yo encuentro un parecido con un amigo mío llamado Luis Flores, quizá mi cerebro haga automáticamente una inferencia y me nazca preguntarle a Jorge: “¿no tienes un hermano llamado Luis?”. Ese tipo de inferencias las puede hacer Prolog, como en el siguiente ejemplo:

padre(juan, manuel). /* el padre de juan es manuel */
padre(pedro, manuel). /* el padre de pedro es manuel */
hermanos(X,Y) :- /* X y Y son hermanos si tienen el mismo padre */
  padre(X,Z),
  padre(Y,Z),
  X<>Y,
  write(X, “es hermano de “, Y).

La regla se lee de la siguiente manera: “X y Y son hermanos si: el padre de X es Z, y el padre de Y es Z, y X no es Y”. Nótese que no se dice en ninguna parte que pedro y juan son hermanos. Prolog, a través de la regla definida, llega a esa conclusión.

Es importante hacer la aclaración de que X no es Y, sino el programa reportaría que X es hermano de sí mismo.

Prolog resuelve todo a través de un motor de inferencias, también reconocido como algoritmo de Robinson (en honor al autor que publicó por primera vez el mecanismo en 1968). De esta manera y abreviando el asunto, en Prolog describimos el problema y el lenguaje nos da las soluciones a través de dos mecanismos: la recursión y el backtrack.

La recursión es simplemente llamarse a sí mismo. En términos de programación significa que una rutina se llame a sí misma hasta que cierta condición impida que se cicle eternamente.

El backtrack consiste en regresar sobre nuestros pasos si resulta que la solución hallada no cumple con nuestras expectativas. Un ejemplo simple de backtrack puede verse en el recorrer un laberinto. Caminamos dentro de éste hasta que topamos con pared. Si esto ocurre, entonces retrocedemos sobre nuestros pasos hasta encontrar la primera bifurcación posible. Seguimos este procedimiento hasta hallar la salida.

Regresando a los cuadrados mágicos, veamos la creación de un cuadrado mágico de orden 3. El listado 1 muestra código en Prolog que resuelve este problema. Todo consiste en describir las condiciones iniciales y las de frontera. Luego le pedimos a Prolog que nos dé las soluciones a través de probar todas las posibilidades exhaustivamente (el árbol solución).

Listado 1. Encontrar cuadrados mágicos con Prolog.

El código del listado 1 básicamente hace lo siguiente:

• Elegir 9 números (todos diferentes).
• Hacer las combinaciones de dichos números —en las ecuaciones correspondientes— que entreguen un resultado R. Este resultado debe ser igual en todas las ecuaciones.
• Si se logra esto, escríbase la solución.
• Búsquese una nueva solución a través de backtrack (aplicando la instrucción fail).

El algoritmo es no determinista, es decir, no sabemos de antemano cuál será el resultado de la ejecución y el sistema, a las mismas entradas, puede dar muchos resultados posibles.

La forma más sencilla de ejecutar este código es por medio de SWISH, que es un ambiente de ejecución de Prolog que funciona en el navegador web. Simplemente entra a http://swish.swi-prolog.org, crea un programa nuevo, pega el código fuente y en la sección donde pones tu query teclea “cuadrado” y da clic a “Run”. El sistema comenzará a calcular e irá desplegando matrices conforme las encuentre.

Como verás, el programa en Prolog es relativamente compacto y simple de entender. Intenta hacer esto en otro lenguaje y verás que tendrás código más grande y complejo. Por otro lado, un inconveniente es que Prolog dista de ser un lenguaje eficiente. En este caso hicimos el cálculo de un cuadrado de un orden relativamente pequeño (3), pero conforme vayamos aumentando el orden, el consumo de memoria aumentará significativamente y podríamos agotarla. Sin embargo, lo importante en este caso es la posibilidad de que, dando solamente los hechos y reglas relevantes, el programa busque con el algoritmo de Robinson, todas las posibles soluciones.