¿Cuáles son las Palabras Diferentes en el Quijote? Un ejercicio con árboles binarios

El Quijote, de Cervantes Saavedra, es uno de los libros más importantes de la literatura mundial. Pensando sobre el Quijote recientemente, se me ocurrió preguntarme ¿cuántas palabras distintas tendrá y cuáles son? El reto por sí mismo es interesante y en el camino se pueden aprender muchas cosas. Veamos a continuación cómo podríamos resolverlo.

La problemática se centra en la estructura de datos a usar. Por ejemplo, imaginemos que queremos usar un arreglo de palabras para irlas acomodando conforme las vamos leyendo. El primero problema con esto es que no sabemos el total de palabras que hay por lo cual ¿de qué tamaño haremos el arreglo? Bueno, si el Quijote (como está en el Proyecto Gutenberg) tiene unas 2 millones de letras, es razonable pensar que un 20% máximo serán palabras, más o menos 400 mil palabras. Podemos crear un arreglo de 400,000 palabras y esperar que esto sea suficiente, pero
definitivamente esta no es una solución ideal.

Una mejor opción es usar estructuras de datos dinámicas, que van creciendo conforme lo vamos requiriendo. Dicho de otra manera, si necesitamos una nueva variable para alojar un dato, creamos esa variable en tiempo de ejecución.

Una estructura de datos dinámica muy poderosa, es la de los árboles binarios. En una estructura de esta naturaleza tenemos un nodo y dos ramas. En el nodo tenemos la información y en las ramas tenemos apuntadores a otros nodos o bien a nulo.

Para explicar cómo funciona una estructura de árbol binario, imaginemos que tenemos la siguiente lista de números desordenada: 60, 41, 74, 16, 53, 65, 25, 46, 55, 63, 70.

Comenzamos tomando el primer valor (60) y usándolo como nodo raíz. Ahora tomamos el siguiente número (41) y lo comparamos al raíz. Dado que es menor que el raíz, y el raíz todavía no tiene rama izquierda, colocamos el 41 en la rama izquierda del 60 (si hubiera sido mayor lo colocaríamos en la rama derecha). El siguiente número es el 74, así que lo ponemos en la rama derecha del 60. A continuación tenemos el 16, dado que el nodo 60 ya tiene rama izquierda (41), entonces ahora bajamos al nodo 41 y comparamos contra este. 16 es menor que 41, y 41 todavía no tiene rama izquierda así que ahí ponemos al 16. De esta forma generamos nuestro árbol, como se muestra en la figura 1.

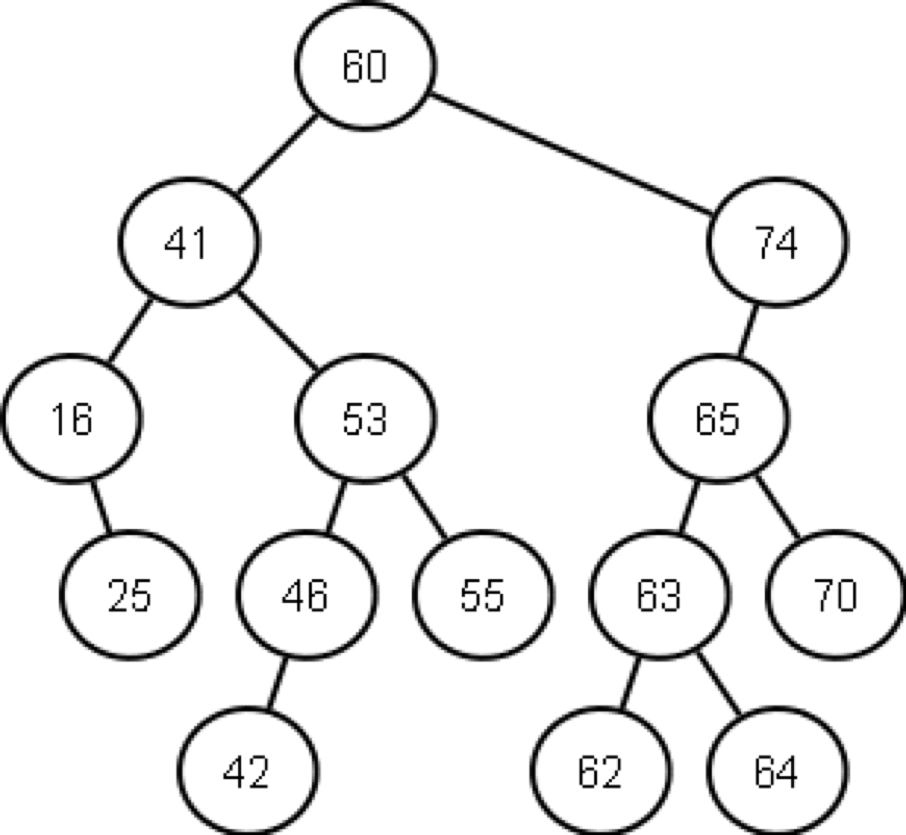
Figura 1. Ejemplo de un árbol binario.

Nótese que un árbol de esta naturaleza además nos da una manera intrínseca de ordenar información. Si queremos desplegar los números que están en este árbol de manera que queden ordenados de menor a mayor, lo que hacemos es muy simple: Partimos del nodo raíz y nos movemos hasta la última rama izquierda posible.

Esto nos dará, de acuerdo a la imagen que hemos puesto, en el número 16. Entonces vemos si este nodo tiene rama derecha. Sí, la tiene, y es el 25. Entonces ponemos como primer número el 16 y después el 25. Nos hacemos un nodo atrás y hallamos el 41. Lo ponemos. Vemos si tiene rama derecha. Sí, la tiene, es el 53, pero éste tiene una rama izquierda, que es el 46 y este nodo a su vez tiene la rama izquierda con el valor 42. Entonces ponemos el 42, 46, 53 y ahora revisamos la rama derecha y hallamos que hay un 55. Por lo tanto la lista va quedando así: 16, 25, 41, 42, 46, 53, 55... Y ahora ya no hay más ramas izquierdas que revisar. Pasamos a la rama derecha del nodo raíz y hallamos que hay un 74. Pero éste tiene un nodo izquierdo, el 65, que a su vez tiene otro, el 63, que a su vez tiene otro más, el 62, por lo que pondremos, 62, 63 y ahora vemos si hay nodo derecho. Y sí, lo hay, el 64. Ponemos ahora el 65 y como tiene rama derecha, ponemos el 70 y finalmente el 74.

Si queremos ordenar el árbol de los números mayores a los menores, lo que tenemos que hacer es recorrer el árbol al revés, primero empezar por la rama derecha. Esto es increíble. La misma estructura nos permite ya dejar ordenados literalmente los datos sin necesidad de otras estructuras.

Pues bien, una vez que tenemos esto aclarado, podemos crear un árbol binario con las palabras del Quijote. Si es una nueva palabra, creamos el primer nodo. Si es una palabra que es menor que la palabra que está en el nodo raíz, la ponemos en un nuevo nodo, que cuelga de la rama de la izquierda, en caso contrario, de la rama derecha.

Pero ¿cómo puedo crear una estructura de un árbol binario? La manera más simple es crear una estructura dinámica, que crece en la medida que lo necesitamos. El listado 1 muestra el código para hacerlo. El código está en Delphi (Pascal) que yo sé que ya no es común ver, pero sirve bien para este propósito.

Listado 1. Estructura de un árbol binario.

Esta definición siempre parece costar trabajo leerla, y la razón es que es la única vez que Pascal permite usar algo que aún no hemos definido. Así, nodoptr = ^nodo; pero node no ha sido aún definido. De hecho, se define inmediatamente después.

Una vez teniendo la estructura dinámica, Delphi (Pascal), nos permite crear una nueva instancia de la misma si la necesitamos. Por ejemplo, definamos

var
    arbol : nodoptr;


Esto es precisamente el árbol en donde iremos colocando las palabras que vayamos leyendo del Quijote. Necesitamos para ello, un procedimiento para insertar nuevos nodos y poner los valores en los mismos.

Listado 2. Rutina para insertar nodos en el arbol

Esa es la rutina imprescindible para ir creando los nodos (con sus respectivas ramas izquierda y derecha). Ahora hagamos la tarea: leamos el archivo del Quijote. Cada línea puede contener un número finito de palabras. El listado 3 tiene el código que abre el archivo de texto a analizar e itera sobre su contenido, línea por línea.

Listado 3. Leemos el archivo e insertamos palabras al arbol

Ejecutar este programa nos arroja que el Quijote tiene 384,123 palabras en total, aunque muchas de ellas se repiten a lo largo de la obra (¿diferentes? unas 30 mil). El programa crea un archivo con todas las palabras (una por línea) y las despliega en orden alfabético. La rutina que crea este archivo se muestra en el listado 4.

Listado 4. Desplegar contenidos del árbol.

Nótese que esta es una rutina recursiva (se llama a sí misma), que permite imprimir todas las palabras diferentes del Quijote en un archivo.

Siguientes pasos

No basta con saber cuáles son las palabras diferentes en total que tiene el Quijote, sino también su frecuencia. Aquí necesitamos entonces hacer dos cosas. La primera es que el nodo contenga no sólo la palabra del texto, sino las veces que la vamos encontrando, algo así como una variable que vaya incrementándose cada vez que encontremos dicha palabra. Por ello, requerimos de un procedimiento más: uno que busque un nodo y pueda modificar los valores del mismo. No lo voy a hacer aquí. Si el amable lector me ha seguido hasta este punto, seguro puede hacer fácilmente esta rutina ¿verdad?