Desarrollo y Simulación de Algoritmos Basados en Temple Cuántico

El algoritmo de Temple Cuántico (TC) —en inglés, quantum annealing— es uno de los paradigmas del cómputo cuántico que más aplicaciones ha encontrado desde el plegado de proteínas, lógica matemática, visión por computadoras, entre otras [1,2]. El TC se basa en las propiedades de la mecánica cuántica y hace uso del fenómeno físico de túnel cuántico para explorar el espacio de soluciones de un problema de optimización combinatorio [3].

Uno de los líderes en tecnología cuántica que han aprovechado el algoritmo de TC es la empresa canadiense D-Wave Systems [4], cuyas computadoras cuánticas actualmente son utilizadas por distintos laboratorios de alto perfil para abordar aplicaciones y estudios teóricos en áreas como: machine learning, exploración espacial, optimización combinatoria, biología, teoría de gráficas, entre otras.

Los avances teóricos se han centrado en estudiar el comportamiento de la evolución del algoritmo de TC para acelerar el proceso de búsqueda de soluciones. Mientras que los avances experimentales y de aplicación se han enfocado en determinar cuáles problemas son más susceptibles de ser resueltos usando TC dadas las limitaciones de hardware cuántico actual.

Recordemos que la unidad de procesamiento más pequeña en una computadora cuántica es el qubit. Un qubit, a diferencia de su contraparte clásica el bit, puede estar tanto en 0/1 como en una superposición entre ambos valores. En el caso del hardware cuántico de D-Wave, los qubits se encuentran interconectados en la llamada topología Chimera. La Figura 1 muestra la topología del procesador D-Wave One el cual tiene 128 qubits. En esta topología, para cualquier qubit q se le asocia un coeficiente h(q) que representa la magnitud de un campo magnético transversal y para cualquier pareja de qubits q1 y q2, se les asocia un coeficiente J(q1,q2) que representa la fuerza de acoplamiento entre q1 y q2. De esta manera, la programación de un procesador cuántico de D-Wave consiste en configurar los coeficientes h(q) y J(q1,q2) para cada qubit q y todas las parejas de qubits q1 y q2, respectivamente.

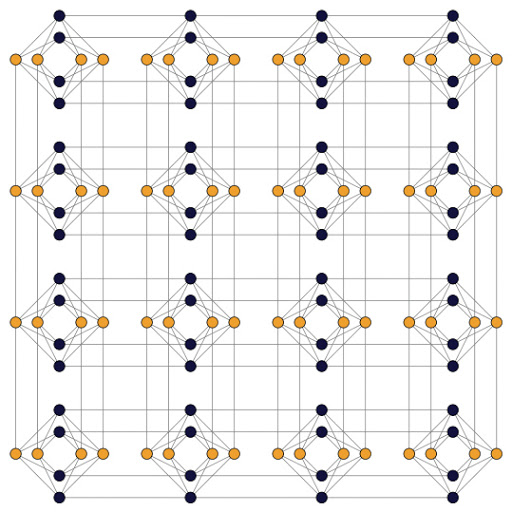
Figura 1. Topologia del procesador cuantico D-Wave One.

Una vez configurados los coeficientes h(q) y J(q1,q2), se lleva a cabo el proceso del algoritmo de TC, el cual hace evolucionar los estados de los qubits. Finalmente, se lleva a cabo una medición cuántica la cual hace que los estados de los qubits “colapsen” a estados clásicos 0/1. El argumento principal del TC es que si el tiempo de evolución del sistema cuántico es lo suficientemente largo, la energía final del sistema será la más baja, y la configuración final de los qubits representa una solución a un problema. La energía del sistema es la suma de los términos q*h(q) y q1*q2*J(q1,q2) para todos los qubits q y todas las parejas q1 y q2. Los tiempos de evolución que se pueden establecer en el hardware cuántico están entre 10 y 100 microsegundos. Dado que el proceso de medición cuántica es un evento probabilístico, se tienen que realizar varias ejecuciones del algoritmo TC con las mismas condiciones iniciales, y el resultado final se toma por votación.

Consideremos cada una de las etapas en la solución de un problema de optimización usando el algoritmo de TC:

1. Un problema de interés en teoría de gráficas es el Máximo Conjunto Independiente (MCI). Una gráfica es una pareja G=(V,E) donde V={1,2,...,n} es un conjunto de vértices y E={e1,e2,...,em} es un conjunto de aristas o parejas de vértices (ver figura 2). Un subconjunto A contenido en V es independiente si para todo par de vértices i,j en A, la pareja {i,j} no forma una arista en E. Así, dada un grafica G=(V,E), el problema MCI consiste en encontrar el conjunto independiente A más grande en G.

2. Para representar de manera lógica el problema MCI asociamos variables booleanas xj a los vértices j tal que j (no) pertenece al conjunto A si xj = 1 (0) para j=1,...,n. Así, por cada posible combinación de valores para x1,...,xn se le asocia un conjunto A que consiste de los vértices j para los cuales xj=1 con j=1,...,n. La cardinalidad del conjunto A coincide con la suma x1 +...+ xn y A es independiente si se cumple que para toda arista {i,j} en E, el producto xi*xj = 0. De este modo, el problema MCI se puede ver como la minimización de una función de energía E(x1,...,xn) como se muestra en la Figura 2.

3. El hardware cuántico D-Wave se diseñó con el objetivo de minimizar funciones de la forma E(x1,...,xn) con términos lineales y por pares. La representación cuántica de la función E(x1,...,xn) consiste en encontrar una correspondencia entre los términos por pares con una o más parejas de qubits en la topología Chimera. La Figura 2 muestra una incrustación del problema en la topología Chimera.

4. Para la ejecución del algoritmo de TC se establece el tiempo de evolución ta y el número de iteraciones que se repetirá el proceso. Por cada iteración se obtiene como resultado un valor de energía y una configuración de los qubits involucrados en la representación del problema. Las soluciones de un algoritmo de TC se interpretan dependiendo del objetivo, ya sea obtener la mínima energía de la función E(x1,...,xn) o encontrar una configuración de los qubits tal que satisfagan una propiedad específica. Por ejemplo, para el ejemplo de la Figura 2, la mínima energía es de 4 y el número de veces que aparece es 781 de 1000 iteraciones. Por lo que la probabilidad de éxito del algoritmo es p=781/1000.

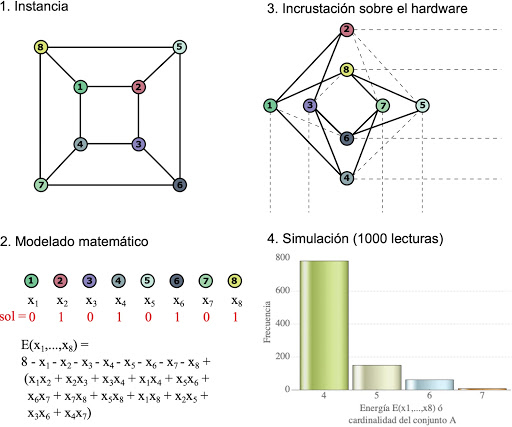
Figura 2. Etapas para la solución de problemas usando el algoritmo de TC.

Estas tecnologías cuánticas han propiciado un nicho de oportunidades en la investigación científica básica. Por ejemplo, algunas de las problemáticas en cada una de las etapas son las siguientes: (1) determinar a qué clase de problemas se pueden encontrar ventajas en la solución de problemas en comparación con los mejores algoritmos clásicos conocidos; (2) encontrar para cada problema de interés la mejor representación matemática con el menor número de variables lógicas; (3) obtener la representación física sobre la topología del hardware cuántico que requiera el menor número de recursos físicos; y (4) amplificar la probabilidad de éxito para encontrar soluciones a un problema dado usando el menor número de repeticiones.

Referencias

[1] Salvador E. Venegas-Andraca, William Cruz-Santos, Catherine McGeoch & Marco Lanzagorta, A cross-disciplinary introduction to quantum annealing-based algorithms, Contemporary Physics, Vol. 59(2), pp. 174—197 (2018).

[2] William Cruz-Santos, Salvador E. Venegas-Andraca & Marco Lanzagorta, A QUBO formulation of the stereo matching problem for D-Wave quantum annealers, Entropy, Vol. 20(10), pp. 786 (2018).

[3] Tadashi Kadowaki & Hidetoshi Nishimori, Quantum annealing in the transverse Ising model, Physical Review E, Vol. 58(5), pp. 5355—5363 (1998).

[4] https://www.dwavesys.com  

[5] Rupak Biswas et al., A NASA perspective on quantum computing: opportunities and challenges, arXiv:1704.04836v1 (2017).

[6] Thomas E. Potok et al., A Study of Complex Deep Learning Networks on High Performance, Neuromorphic, and Quantum Computers, arXiv:1703.05364v2 (2017).