La prueba de software y los special purpose languages

PARTE 6. Máquinas Abstractas y Lenguajes 

Comenzamos abordando los lenguajes formales de una manera más bien no-procedural, en términos algebraicos y de conjuntos; después lo hicimos de una forma más procedural, utilizando gramáticas. En este número los abordaremos con un enfoque muy procedural, mediante Máquinas de (Conjuntos de) Estados Finitos (o Finite States Machines), MEFs.

Pero antes de continuar: dado que en el número anterior no aparecieron referencias bibliográficas, las anexo al final de esta columna. Si quisieran profundizar en lo que abordaremos en este número, pueden consultar algún texto sobre Análisis y Diseño de Algoritmos (en particular la sección de NP-Completeness). Y (como creo haber dicho) si quisieran ahondar en los otros temas que hemos abordado pueden consultar textos sobre Autómatas y Lenguajes Formales y Compiladores.

Sin pretensión de tratar de ser exhaustivos aquí, y limitándonos solo a la formalidad suficiente para poder ser claros (aunque sacrificando precisión), vayamos a nuestro tema.

Máquinas de (Conjuntos de) Estados Finitos (MEFs)

Las Máquinas de Turing (ver definición más adelante) son un tipo de MEFs con las que se abordó la cuestión de la “computabilidad” (otro enfoque fueron las funciones recursivas), tratando de descubrir los alcances y las limitaciones de las máquinas (computadoras) que estaban construyéndose/por construirse (Turing publicó su trabajo más importante en 1936).

Las MEFs que presentaremos aquí tienen en común que:

• están constituidas por un conjunto finito de estados en los que la MEF puede encontrarse cuando procesa la cadena de entrada; hay un estado inicial en que la MEF comienza su procesamiento y un estado (o más, dependiendo del tipo de MEF) en el (los) que puede terminarlo;

• los símbolos que conforman la cadena de entrada son elementos de un conjunto finito (el “Alfabeto”);

• las operaciones de la MEF se definen mediante una relación (en el sentido matemático) de transición ρ  , que toma el estado en el que se encuentra la MEF en ese momento y el símbolo actual de la cadena de entrada (y, como veremos, eventualmente otras cosas, dependiendo del tipo de MEF), y regresa el estado al que la MEF debe moverse (y eventualmente otras cosas, como veremos); si la relación de transición ρ  es una función (en el sentido matemático), entonces se le denota con δ y se dice que la MEF es determinística, en caso contrario se denota con ρ  y se dice que es no-determinística.

Aquí usaremos dos convenciones: a) considerar que la MEF termina su procesamiento indicando que no acepta la cadena de entrada cuando alcanza una transición en la relación/función de transición que no haya sido explicitada; y b) mostraremos la MEF mediante un grafo, en el cual los nodos serán los estados y en las aristas colocaremos los elementos que terminen de definir las transiciones de la relación/función de tansición.

Veamos ahora las MEFs particulares.

Autómatas Finitos (AFs)

Los AFs (ó Finite Automata) se definen como quíntuples de la forma      AF = 〈S,ι, F, A, ρ 〉 ,     en los cuales    

S    es el conjunto de eStados,                                 ι  ( ∈S ) es el estado inicial,

F   ( ⊂S ) es el conjunto de estados Finales,        A   es el Alfabeto del lenguaje de la cadena de entrada,   y  

ρ  (ó δ )  es la Relación (ó Función) de transición    ρ (ó δ ) : ( s1, a  )→  s2 , para    s1, s2 ∈ S,   a ∈ A.

Como podrá verificarse, el siguiente AF es determinístico y procesa el lenguaje    am bn eidk  ,  para m, n, i, k  ≥1 e independientes entre sí.

El AF inicia el procesamiento en el estado ι; lee una a  de la cadena de entrada y pasa al Estado 1, en el cual lee cero más  a’s (la transición es un ciclo); después procesa una o más  b’s (al menos una), luego una o más  e’s (al menos una), y finalmente una o más  d’s (al  menos una). Siguiendo nuestra convención, si nos encontráramos en el Estado 2 y en la cadena de entrada no tuviéramos una b o una c el autómata no aceptaría la cadena y terminaría su procesamiento.

Se ha demostrado que los AFs procesan solamente los Lenguajes Regulares (pero todos ellos). En particular, no pueden procesar los Lenguajes Libres de Contexto porque no tienen memoria que les permita empatar caracteres por pares, como lo requieren este tipo de lenguajes.

Se ha demostrado también que en el caso de los AFs el no-determinismo no implica mayor poder de procesamiento.

Igualmente, se ha demostrado que para cada Expresión Regular existe un AF que procesa el mismo lenguaje y viceversa (de hecho, lo usual es que las herramientas que procesan textos mediante Expresiones Regulares primero las transformen en AFs  –como las usadas para definir analizadores léxicos lex y flex).

Autómatas de Pila (APs)

Los APs (ó Push Down Automata) se definen como séxtuples de la forma    AP = 〈S,ι, F, A, Σ, ρ 〉,    en los cuales   

S    es el conjunto de eStados,            ι    ( ∈S ) es el estado inicial,

F  ( ⊂S ) es el conjunto de estados Finales,                      A   es el Alfabeto del lenguaje de la cadena de entrada,   

Σ   es el alfabeto de la pila (o Stack), que es el tipo de memoria que tienen los APs  ( #∈Σ , A ⊂Σ  ) ,   y  

ρ  (ó δ)es la Relación (ó Función) de transición  ρ (ó δ) : ( s1, a, σ1 ) → ( σ2 , s2), para s1, s2 ∈ S, a ∈ A, σ1, σ2∈Σ.

Como podrá verificarse, el siguiente AP es determinístico y procesa el lenguaje     ai bn end i  ,  para n, i≥  1.

Iniciamos en ι y pasamos al Estado 1 sin leer símbolos la cadena de entrada (eso significa la primera λ de la primera transición), no sacamos elemento alguno de la pila (eso significa la segunda λ) y metemos “#” a la pila.

Del Estado 1 pasamos al Estado 2 leyendo una a de la cadena de entrada sin sacar elemento alguno de la pila y metiendo una a a la pila. En el Estado 2 repetimos cero o más veces lo siguiente (la transición es un ciclo): leer una a de la cadena de entrada, no sacar elemento alguno de la pila y meter una a a la pila.

En las siguientes transiciones (hasta la del Estado 3) ejecutamos un proceso semejante al anterior pero ahora con las b´s: por cada b que leemos de la cadena metemos una b a la pila.

Las 2 transiciones subsiguientes (hasta la del Estado 4) se ocupan de sacar una b de la pila por cada e que se lee de la cadena de entrada.

Las 2 transiciones subsiguientes (hasta la del Estado 5) sacan una a de la pila por cada d que lean de la cadena de entrada.

La última transición no lee elemento alguno de la cadena de entrada y saca el # de la pila sin meter elemento alguno en ella.

Se ha demostrado que los APs procesan solamente los Lenguajes Libres de Contexto (pero todos ellos). En particular, no pueden procesar los Lenguajes Sensibles al Contexto porque la pila sólo les permita empatar caracteres por pares anidados y no en tercias o por pares no anidados, como lo requieren algunos lenguajes de este tipo.

También se ha demostrado que para los AP el no-determinismo sí implica mayor poder de procesamiento, por lo que en los Lenguajes Libres de Contexto (LLC) tenemos los LLC no-determinísticos englobando a los LLC determinísticos.

Un caso concreto es el lenguaje    ai bi∪ ai b2i  ,  para m, i  ≥  0   que es un LLC para el que no existe un AP determinístico que lo procese.

Igualmente, se ha demostrado que para cada Gramática Libre de Contexto existe un AP que procesa el mismo lenguaje, y viceversa (de hecho, lo usual es que las herramientas que procesan ese tipo de gramáticas (“determinísticas”) primero las transformen en APs (determinísticos)  –como las usadas para definir analizadores sintácticos yacc y bison).

1. Máquinas de Turing (MTs)

Las MT (ó Turing Machines) se definen como séxtuples de la forma    MT = 〈S,ι, h, A, Γ, ρ 〉,    en los cuales   

S    es el conjunto de eStados del AF,                                        ι    ( ∈S ) es el estado inicial,

h   (∈S ) es el estado Final,                                                          A   es el Alfabeto del lenguaje de la cadena de entrada,   

Π  es el alfabeto de la cinta de Procesamiento, el tipo de memoria que tienen las MTs    ( #, $∈Σ ; A ⊂Π   ),    y   

ρ  (ó δ)es la Relación (ó Función) de transición  ρ (ó δ) : ( s1, π1 ) → ( π2 ,μ, s2), para    s1, s2 ∈ S,    π1 , π2 ∈Π,

μ = L (mover la cabeza a la celda de la derecha) ó μ = R (moverla a la de la izquierda).

En el caso de las MT tomaremos la convención de que la cadena de entrada se coloca en la cinta de la siguiente manera: primero se coloca un “#”, luego la cadena de entrada, y un “$” después de ella.

Se ha demostrado que las MTs procesan solamente (pero todos) los Lenguajes Estructurados por Frases (o “Recursivamente Enumerables”). En particular, no pueden procesar los Lenguajes Generales (así como no son susceptibles de ser definidos con reglas, tampoco lo son de ser procesados por máquinas).

En el caso de las MTs el no-determinismo no implica mayor poder de procesamiento.

Los trabajos con las MTs han dado lugar a lo que se conoce como la Tesis de Turing:

   Las MTs modelan exactamente lo que pueden realizar las computadoras.

Esta Tesis es muy relevante y útil: aún cuando (se asume que) las MTs tienen el mismo poder de procesamiento que las computadoras, estas máquinas abstractas son muy simples en su funcionamiento, lo cual facilita realizar demostraciones sobre las capacidades y limitaciones de las computadoras.

En las MT tenemos varias clases muy importantes, que procedemos a revisar.

2. Autómatas Delimitados Linealmente (ADLs)

Los ADLs (ó Linear Bounded Automata) son MTs que para procesar una cadena solo requieren una cantidad de celdas en la cinta de procesamiento prácticamente igual a la de la cadena de entrada. Los ADLs pueden procesar los Lenguajes Sensibles al Contexto.

Como podrán verificar, el siguiente ADL es determinístico que procesa el lenguaje    ai bn eid n  ,  para n, i≥1 .

La MT inicia en ι y pasa al Estado 1 leyendo el “#” que antecede a la cadena de entrada, escribiendo el mismo “#” y moviéndose a la celda de la derecha.

Del Estado 1 pasa al Estado 2 leyendo una a de la cadena de entrada, escribiendo una A y moviéndose a la derecha.

En el Estado 2 podemos repetir cero o más veces algunas de las siguientes operaciones (en realidad deberíamos dibujar 3 ciclos en el autómata, uno para cada transición, pero por motivos de espacio dibujamos solo uno y apilamos las transiciones):

1. leer una a de la cadena de entrada, escribir una a y moverse a la derecha (o sea: nos saltamos las a’s);

2. leer una b de la cadena de entrada, escribir una b y moverse a la derecha (nos saltamos las b‘s);

3. leer una E de la cadena de entrada, escribir una E y moverse a la derecha (nos saltamos las E’s).

Después pasamos al Estado 3 leyendo la primera e, transformándola en E y moviéndonos a la izquierda; luego nos movemos hacia la izquierda saltándonos todas las a’s, b’s, y E’s hasta encontrar una A, nos movemos a la derecha y llegamos nuevamente al Estado 1.

Enseguida podemos repetir cero o más veces las operaciones de las transiciones de los Estados 1, 2 y 3, las cuales se pueden resumir como “cambiar una e por E por cada a que se haya cambiado antes por A” (con ello verificamos si hay igual cantidad de a‘s que de e‘s). Dejamos de hacer eso cuando encontramos una b; entonces escribimos b, nos movemos a la izquierda y vamos al Estado 4. Leemos una A, escribimos una A y vamos al Estado 5.

En las transiciones de los Estados 5, 6 y 7 realizamos con y las b‘s y d‘s algo semejante a lo que hicimos con las a‘s y e‘s en los los Estados 1, 2 y 3: “cambiar una d por D por cada b que se haya cambiado antes por B” para verificar si hay igual cantidad de b‘s que de d‘s. Dejamos de hacer eso cuando encontramos una E; entonces escribimos una E, nos movemos a la izquierda y vamos al Estado 8, donde nos saltamos todas las D‘s y E‘s moviéndonos a la derecha hasta encontrar el #  que debe venir después del final de la cadena de entrada.

3. Máquinas de Turing que terminan (MTtsterm) – Algoritmos

Las MTsterm son MTs que siempre terminan cuando procesan cualquier cadena  –aunque eventualmente después de mucho tiempo.  Las MTsterm pueden procesar los Lenguajes Decidibles (o “Recursivos”).

La penúltima frase puede parecer obvia, especialmente con tanta ciencia ficción y con tan altas expectativas puestas sobre la nouvelle Artificial Intelligence, pero ocurre que hay problemas que una MT simplemente no puede resolver (y, de acuerdo a la Tesis de Turing, tampoco las computadoras). Un ejemplo es la demostración de teoremas en el Cálculo de Predicados de Primer Orden, que describiremos aquí rápida e informalmente: desde hace décadas tenemos sistemas de inferencia (finalmente, MTs) que pueden generan todos los teoremas en ese Cálculo; inicialmente se pudo pensar que, para saber si una fórmula era un teorema, simplemente bastaría con comparar esa fórmula con cada uno de los teoremas que fuera generando el sistema;  y efectivamente, si la fórmula es un teorema, en algún momento (quizás en un día, quizás en 1,000,000 de años) el sistema anunciará que encontró un teorema que es equivalente a nuestra fórmula; sin embargo, si la fórmula no es un teorema, el sistema (la MT) nunca terminará porque no generará un teorema equivalente a nuestra fórmula.

A partir de algo como lo anterior, es que se suele definir Algoritmo como una MT que siempre termina (MTterm).

Problemas, Algoritmos y Heurísticas

Ahora bien: hay problemas para los cuales no se han encontrado algoritmos eficientes que los resuelvan (y se presume que no existen). En esos casos se suele optar por abstenerse de buscar la solución óptima mediante la revisión de todas las alternativas en el grafo de búsqueda, y en su lugar recorrer solo parte de él para encontrar buena solución. A estos métodos solemos llamarlos Heurísticas.

Para ejemplificar lo anterior tomemos el Problema del Vendedor Viajero (PVV): Un Vendedor debe visitar n-1 ciudades partiendo de una inicial, considerando que viajar de una ciudad a otra tiene un costo asociado.

El PVV se puede modelar mediante un grafo dirigido con pesos en las aristas.

Sabemos que, dado un grafo dirigido con n nodos, la cantidad máxima de aristas (dirigidas) es n (n+1), pero: cuántas rutas hay en ese grafo? Eso nos permitiría saber cuántas rutas tenemos que comparar para escoger la de costo mínimo.

Para simplificar nuestro análisis, pensemos que el costo para ir a de una ciudad a otra es el mismo de ida que de vuelta. Tenemos entonces un grafo no dirigido con n nodos, por lo cual la cantidad máxima de aristas es   n (n+1) / 2 .  Ahora bien, cuando el grafo…

• tiene 3 nodos, partiendo del nodo inicial solo tenemos 2 rutas para visitar los otros 2 nodos.

• tiene 4 nodos, partiendo del inicial podemos iniciar 3 rutas yendo a cada uno d los otros 3 nodos, y entonces nos quedan 2 nodos por visitar en cada caso que como vimos en el punto anterior, genera 2 rutas cada uno; por tanto tendríamos 6 rutas.

• tiene 5 nodos, partiendo del inicial podemos iniciar 4 rutas yendo a cada uno d los otros 4 nodos, y entonces nos quedan 3 nodos por visitar en cada caso que como vimos en el punto anterior, genera 2 rutas cada uno; tendríamos entonces 24 rutas.

Supongamos que en general, si el grafo tiene n nodos, habrá n! ( = 1*2*3*…*n ) rutas.

En la siguiente tabla se muestran los valores para las curvas    log2 n  (la búsqueda en un árbol binario con n datos requiere una cantidad de operaciones múltiplo de log2 n  ),    n  ,    n 2  (ordenar  n datos con el método de “Burbuja” requiere una cantidad de operaciones múltiplo de n 2  ), y   2 n   .  (  n!  •2 n a partir de  n=4 ).

Los numeros en azul son aproximaciones mías (suficientemente acertadas para nuestro propósito); el resto los produjo la computadora. (El primero de ellos se leería “uno por diez elevado a la tres por diez elevado a la 2” = 1*10 300  ).

Hoy hablamos de Internet of Things, y de BIG Data. Supongamos que nos topamos con un problema equivalente al PVV con una cantidad de ciudades igual a 109 . (Si cada ciudad se llevara un Byte, entonces estamos hablando de un GigaByte, nada extraordinario en BIG Data).

Para hacer nuestro análisis sin problemas de desbordamiento, tomemos valores no de  n!  sino de  n2  (para n=100,  n! vale casi 10158 ). Haciéndolo así, con un GigaByte de ciudades, el algoritmo que revisara todas las rutas para encontrar la óptima tendría que realizar 10300,000,000 operaciones (ver la tabla).  Eso implica mucho, o poco tiempo?

Supongamos que podemos paralelizar mil millones de supercomputadoras que pueden realizar cada una 1021 operaciones por segundo (un millón de PetaFlops). En un año todas ellas podrían realizar 109*365*24*60*60*1021= 109*3.1536 *107*1021 = 3.1536 *1037 operaciones,  así es que (asumiendo que una operación bastara para procesar una ruta completa) para obtener la ruta óptima para un grafo con 109 nodos, el algoritmo del PVV se tardaría  solamente 10300,000,000-37  años.

Esperar a obtener el resultado es, al menos, impráctico. Por supuesto, la estrategia a seguir sería utilizar una Heurística.

Con los elementos del análisis anterior estamos en posición de responder la pregunta que nos había quedado pendiente en un número anterior, acerca de la eficiencia con la que podemos procesar los distintos tipos de lenguajes que hemos venido revisando. La ofrecemos en la siguiente tabla, considerando una cadena de entrada de longitud n (como dijimos al principio, debido a que nos limitamos solo a la formalidad suficiente, es necesario sacrificar precisión):

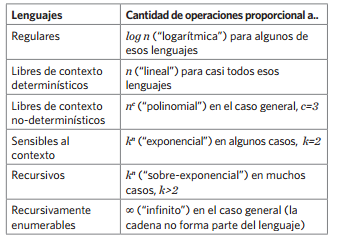
Tabla 2. Eficiencia para probar distintos lenguajes.

Referencias

[1]Luis Vinicio León Carrillo: Traducción de Frases del Español al Francés en un Dominio restringido; Tesis de Licenciatura, ITESO, 1990

[2]Pierre Janton: Einfürhrung in die Esperantologie; Georg Olms, 1993.

[3]Roland Hausser: Foundations of Computational Linguistics; Springer, 1999.